Abstract
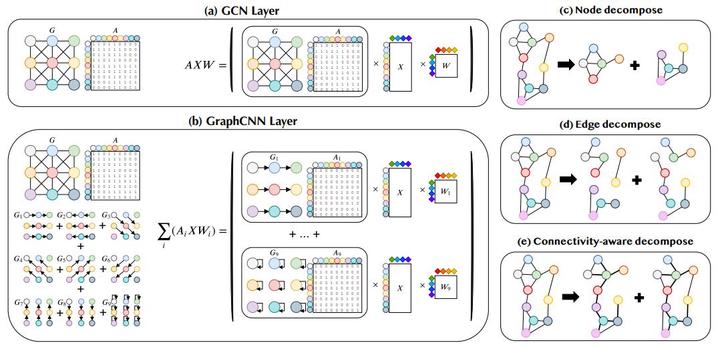
Mining from graph-structured data is an integral component of graph data management. A recent trending technique, graph convolutional network (GCN), has gained momentum in the graph mining field, and plays an essential part in numerous graph-related tasks. Although the emerging GCN optimization techniques bring improvements to specific scenarios, they perform diversely in different applications and introduce many trial-and-error costs for practitioners. Moreover, existing GCN models often suffer from oversmoothing problem. Besides, the entanglement of various graph patterns could lead to non-robustness and harm the final performance of GCNs. In this work, we propose a simple yet efficient graph decomposition approach to improve the performance of general graph neural networks. We first empirically study existing graph decomposition methods and propose an automatic connectivity-ware graph decomposition algorithm, DeGNN. To provide a theoretical explanation, we then characterize GCN from the information-theoretic perspective and show that under certain conditions, the mutual information between the output after l layers and the input of GCN converges to 0 exponentially with respect to l. On the other hand, we show that graph decomposition can potentially weaken the condition of such convergence rate, alleviating the information loss when GCN becomes deeper. Extensive experiments on various academic benchmarks and real-world production datasets demonstrate that graph decomposition generally boosts the performance of GNN models. Moreover, our proposed solution DeGNN achieves state-of-the-art performances on almost all these tasks.